# 3.3 多类别分类
在第 3.2 节中,我们探讨了如何构造二分类问题。现在,我们将快速讨论如何处理非二分类,即涉及三个或更多类的分类任务[58]。我们将说明多类分类的数据集的例子是鸢尾花数据集,这是一个著名的数据集,其起源于统计领域[59]。该数据集集中在鸢尾花的三种物种上,分别称为“iris setosa”, “iris versicolor”和 “iris virginica”。 可以根据它们的形状大小将这三个物种区分开。20 世纪初,英国统计学家罗纳德·费舍尔(Ronald Fisher)测量了 150 个样本的花瓣和萼片(花的不同部分)的长度和宽度。该数据集是平衡的:每个目标标签正好有 50 个样本。 在此问题中,我们的模型将花瓣长度,花瓣宽度,萼片长度和萼片宽度这四个数值特征作为输入,并尝试预测目标标签(三个物种之一)。该示例位于 tfjs-examples 的 iris 文件夹中,您可以使用以下命令检出并运行该文件夹:
git clone https://github.com/tensorflow/tfjs-examples.git
cd tfjs-examples/iris
yarn && yarn watch
# 3.3.1 分类数据的 one-hot 编码
在研究解决分类问题的模型之前,我们需要重点介绍在此多类分类任务中分类目标(物种)的表示方式。到目前为止,我们在本书中看到的所有机器学习示例都涉及简单的目标表示,例如下载时间预测问题和 Boston Housing 问题中的单个数字,以及 0-1 的二进制表示钓鱼检测问题中的目标。但是,在本节问题中,以一种不太熟悉的方式(称为“ one-hot 编码”)来表示这三种花。打开 data.js,您会注意到以下一行:
const ys = tf.oneHot(tf.tensor1d(shuffledTargets).toInt(), IRIS_NUM_CLASSES);
在这里,shuffledTargets 是一个 JavaScript 数组,由示例的整数标签组成,顺序为随机排序。其元素的值分别为 0、1 和 2,反映了数据集中的三个种类。通过 tf.tensor1d(shuffledTargets).toInt()调用将其转换为 int32 类型的 1D 张量。然后将所得的一维张量传递到 tf.oneHot()函数中,该函数返回形状为[numExamples,IRIS_NUM_CLASSES] 的 2D 张量。numExamples 是目标包含的示例数,而 IRIS_NUM_CLASSES 只是常量 3。您可以通过在上面引用行正下方添加一些打印行来检查目标和 ys 的实际值,例如:
const ys = tf.oneHot(tf.tensor1d(shuffledTargets).toInt(), IRIS_NUM_CLASSES);
#Added lines for printing the values of `targets` and `ys`.
console.log('Value of targets:', targets);
ys.print()[60];
进行这些更改后,终端 yarn watch 命令启动打包程序将自动重建 Web 文件。然后,您可以在用于观看此演示的浏览器选项卡中打开 devtool 并刷新页面。来自 console.log 和 print()调用的打印消息将被记录到 devtool 的控制台中。 您将看到的打印消息看起来像这样
Value of targets: (50) [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Tensor
[[1, 0, 0],
[1, 0, 0],
[1, 0, 0],
...,
[1, 0, 0],
[1, 0, 0],
[1, 0, 0]]
要么是
Value of targets: (50) [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Tensor
[[0, 1, 0],
[0, 1, 0],
[0, 1, 0],
...,
[0, 1, 0],
[0, 1, 0],
[0, 1, 0]]
用语言来描述,对于带有整数标签 0 的示例,您将获得一行值[1,0,0]; 对于带有整数标签 1 的示例,您将获得一行值[0,1,0],依此类推。这是一个简单清晰的 one-hot 编码示例:将整数标签转换为由全零值组成的矢量,但与该标签相对应的索引处的值是 1,矢量的长度等于所有可能类别的数量。向量中只有一个 1 值正是将这种编码方式称为“ one-hot”的原因。 这种编码对您来说可能看起来比较复杂。当一个数字可以完成一项工作时,为什么要使用三个数字来表示一个类别?为什么我们选择这种方式而不是更简单,更经济的单整数索引编码?这可以从两个不同的角度来理解。 首先,与整数相比,神经网络输出连续的浮点型值要容易得多。对于神经网络的最后一层,更为优雅自然的方法便是输出一些单独的浮点型数字,通过类似于 sigmoid 激活函数,每个浮点数在[0,1]区间内用于二分类。在这种方法中,每个数字都是模型对输入示例属于相应类别概率的估计。这正是 one-hot 编码的目的:这是概率分数的“正确答案”,模型应针对该分数通过训练过程进行调整。 其次,通过将类别编码为整数,我们隐式地在类之间创建顺序。例如,我们可以将 iris setosa 标记为 0,iris versicolor 标记为 1,将 iris virginica 标记为 2。但是这样的排序方案通常是人为的且不合理的。例如,上面的编号方案意味着 setosa 与 versicolor 比 virginica 更“接近”,这可能不是正确的。神经网络以实数为基础,并基于数学运算,例如乘法和加法。因此,它们对数字的大小及其顺序非常敏感。如果将类别编码为单个数字,则它将成为神经网络必须学习的额外非线性关系。相比之下,one-hot 编码类别不涉及任何隐含的排序,因此不会以这种方式增加神经网络的学习能力。 正如我们将在第 9 章中看到的那样,one-hot 编码不仅用于神经网络输出目标,而且在分类数据形成神经网络的输入时也适用。
# 3.3.2 Softmax 激活
了解了输入要素和输出目标的表示方式后,我们现在就可以查看定义模型的代码。
# 代码 3.8 来自 iris / index.js 的用于鸢尾花分类的多层神经网络的代码
const model = tf.sequential();
model.add(tf.layers.dense({ units: 10, activation: 'sigmoid', inputShape: [xTrain.shape[1]] }));
model.add(tf.layers.dense({ units: 3, activation: 'softmax' }));
model.summary();
const optimizer = tf.train.adam(params.learningRate);
model.compile({
optimizer: optimizer,
loss: 'categoricalCrossentropy',
metrics: ['accuracy']
});
上面定义的模型得出一下参数:
| Layer(类别) | 输出形状 | 参数# |
|---|---|---|
| 密集层 1 | [null, 10] | 50 |
| 密集层 2 | [null, 3] | 33 |
全部参数:83 可训练参数:83 不可训练参数:
从中可以看出,这是一个相当简单的模型,具有相对较少的权重参数(83)。输出形状[null,3] 对应于分类目标的 one-hot 编码。用于最后一层的 softmax 激活是专门为多类分类问题设计的。softmax 定义的数学定义可以编写为以下代码:
softmax([x1, x2, …, xn]) =
[exp(x1) / (exp(x1) + exp(x2) + … + exp(xn)),
exp(x2) / (exp(x1) + exp(x2) + … + exp(xn)),
…,
exp(xn) / (exp(x1) + exp(x2) + … + exp(xn))]
与我们看到的 sigmoid 激活函数不同,softmax 激活函数不是对每个元素进行处理的,因为输入矢量的每个元素都依赖于所有其他元素。具体来说,输入的每个元素都将转换为其自然指数(即以 e = 2.718 为基数的 exp 函数)。然后将指数除以所有元素的指数之和。这是做什么的?首先,它确保每个数字都在 0 到 1 之间。其次,确保输出矢量的所有元素总和为 1。这是一个理想的属性,因为 a)输出可以解释为分配的概率;b)为了与分类交叉熵损失函数兼容,输出必须满足该属性。第三,确保输入向量中的较大元素映射到输出向量中的较大元素。这里给出一个具体的例子,假设在最后致密层经过矩阵乘法和加法产生的向量:
[ -3 ,0 ,-8 ]
其长度为 3,因为致密层配置具有 3 个单位。注意,这些元素是不受任何特定范围限制的浮点数。softmax 激活会将向量转换为:
[ 0.0474107 ,0.9522698 ,0.0003195 ]
您可以通过运行以下 TensorFlow.js 代码来自己验证这一点(例如,当页面指向 js.tensorflow.org 时,在 devtool 控制台中):
const x = tf.tensor1d([-3, 0, -8]);
tf.softmax(x).print();
softmax 函数输出的三个元素是 1)全部在[0,1]中; 2)总和为 1; 3)以与输入向量中的顺序匹配的方式进行排序。由于这些属性,可以将输出解释为(由模型)分配给所有可能类别的概率值。在上面的示例中,第二个类别的概率最高,而第一个类别的概率最低。 当使用这种类型的多类分类器的输出时,可以选择最高 softmax 元素的索引作为最终决策,即,对输入所属类别的决策。这可以通过使用 argMax()方法来实现。例如,这是 index.js 的摘录:
const predictOut = model.predict(input);
const winner = data.IRIS_CLASSES[predictOut.argMax(-1).dataSync()[0]];
predictOut 是二维张量[numExamples,3]。调用 argMax 方法会使形状减小为[numExample]。参数值-1 表示 argMax 应该在最后一个维度上寻找最大值并返回其索引。例如,假设 predictOut 具有以下值:
[[ 0 ,0.6 ,0.4 ], [ 0.8 ,0 ,0.2 ]]
然后 argMax(-1)将返回一个张量,该张量指示在第一个和第二个示例的索引 1 和 0 处分别找到沿最后一个(第二个)维的最大值:
[ 1 ,0 ]
# 3.3.3 分类交叉熵:多分类的损失函数
在二分类示例中,我们看到了如何将二进制交叉熵用作损失函数,以及为什么不能将其他更易于理解的指标(如准确性和召回率)用作损失函数。多类分类的情况非常相似。一个简单的指标,即准确性,该准确性是模型正确分类的示例的一部分。其度量标准对于人类理解模型的性能非常重要,并在清单 3.8 的代码段中使用了该度量标准:
model.compile({ optimizer: optimizer, loss: 'categoricalCrossentropy', metrics: ['accuracy'] });
但是,准确度不是损失函数好的选择,因为它与二分类的准确度一样会遭受零梯度问题。因此,人们为多分类设计了一种特殊的损失函数:分类交叉熵。它只是将二元交叉熵泛化为两个以上类别的情况。
# 代码 3.9 用于分类交叉熵损失函数的代码(此用于单个输入示例)
function categoricalCrossentropy(oneHotTruth, probs):
for i in (0 to length of oneHotTruth)
if oneHotTruth(i) is equal to 1
return -log(probs[i]);
在上面的代码中,oneHotTruth 是输入示例实际类的 one-hot 编码。概率是模型输出的 softmax 概率。上面的代码的关键之处在于,就分类交叉熵而言,概率中只有一个元素很重要,也就是索引与实际类相对应的元素。概率的其他元素可能会有所不同,但只要它们不更改实际类的元素,就不会影响分类交叉熵。对于特定的概率元素,它越接近 1,则交叉熵的值将越低。像二分类的交叉熵一样,多分类交叉熵可以直接用 tf.metrics 命名的函数,使用它来计算简单的分类交叉熵。例如,使用以下代码,您可以创建一个 one-hot 编码 truth label 和一个假设的概率向量,并计算相应的分类交叉熵值:
const oneHotTruth = tf.tensor1d([0, 1, 0]);
const probs = tf.tensor1d([0.2, 0.5, 0.3]);
tf.metrics.categoricalCrossentropy(oneHotTruth, probs).print();
# 表 3.5 不同概率输出下分类交叉熵的值。在不失一般性的前提下,所有示例(行)都基于以下情况:存在三个类别,而实际类别是第二个类别。
| One-hot truth label | 概率(softmax 输出) | 分类交叉熵 | MSE |
|---|---|---|---|
| [0,1,0] | [0.2、0.5、0.3] | 0.693 | 0.127 |
| [0,1,0] | [0.0,0.5,0.5] | 0.693 | 0.167 |
| [0,1,0] | [0.0,0.9,0.1] | 0.105 | 0.006 |
| [0,1,0] | [0.1,0.9,0.0] | 0.105 | 0.006 |
| [0,1,0] | [0.0,0.99,0.01] | 0.010 | 0.00006 |
通过比较上表中的第 1 行和第 2 行或比较第 3 行和第 4 行,应该清楚的是,更改与实际类不对应的概率元素不会更改交叉熵,即使它可能会更改 one-hot 真值标签和 pros,但是会影响 MSE。同样,就像在二元交叉熵中一样,当实际类别的概率值接近 1 时,MSE 的回报率会降低,因此不利于影响正确类别的概率值。这就是为什么分类交叉熵比 MSE 更适合作为损失函数用于多类分类问题的原因。
# 3.3.4 混淆矩阵:多分类的详细分析
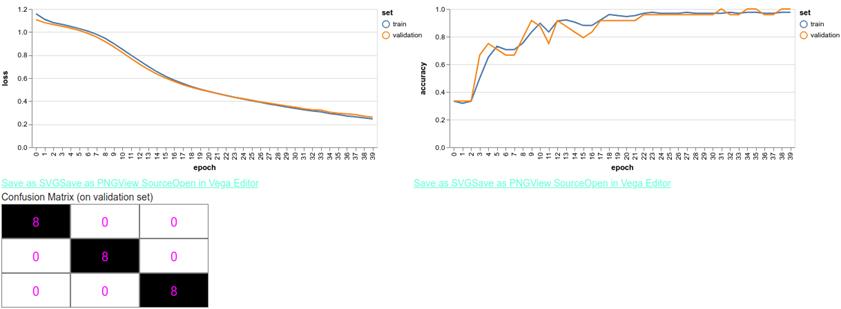
通过单击示例网页中的“Train Model from Scratch”按钮,您可以在几秒钟内获得训练有素的模型。如图 3.9 所示,该模型在经过 40 个训练周期后达到了近乎完美的精度。这反映了 iris 数据集在特征类之间具有相对明确定义的边界。 图 3.9 的底部显示了表征多分类器行为的另一种方式,称为混淆矩阵。混淆矩阵会根据多分类器的实际分类和模型的预测分类来分解结果。它是形状为[numClasses,numClasses]的方阵。索引为[i,j] (行 i 和列 j)的元素是属于类 i 并被模型预测为类 j 的示例数。因此,混淆矩阵的对角元素对应于正确分类的示例。完美的多类分类器应产生一个对角线之外不包含非零元素的混淆矩阵。图 3.9 中的混淆矩阵就是这种情况。
# 图 3.9 训练 iris 模型 40 周期的结果。左上方:针对训练时期绘制的损失函数。右上:相对于训练时期绘制的准确性。下:混淆矩阵。
 除了显示最终的混淆矩阵之外,iris示例还使用onTrainEnd()回调在每个训练时期的末尾绘制混淆矩阵。开始阶段,您可能会看到一些其他类型的矩阵(例如,参见下面的图3.10)。
除了显示最终的混淆矩阵之外,iris示例还使用onTrainEnd()回调在每个训练时期的末尾绘制混淆矩阵。开始阶段,您可能会看到一些其他类型的矩阵(例如,参见下面的图3.10)。
# 图3.10 “不完美”混淆矩阵的示例,其中对角线外有非零元素。在训练收敛之前,仅在2次训练周期后生成此混淆矩阵

图 3.10 中的混淆矩阵表明,在 24 个输入示例中有 8 个被错误分类,这对应于 66.7%的准确度。但是,混淆矩阵告诉我们的不仅仅是单个数字:它显示哪些类涉及最多的错误,哪些类涉及更少的错误。在此特定示例中,所有来自第二类的花都被错误分类(作为第一类或第三类),而来自第一类和第三类的花始终被正确分类。因此,您可以看到,在多类别分类中,混淆矩阵比简单的准确性更能提供更多信息,就像精度和召回率一起构成的分类比二分类的准确性更全面。混淆矩阵可以提供有助于与模型和训练过程相关的决策的信息。比如将体育网站误认为游戏网站,可能比将体育网站混淆为网络钓鱼诈骗更是一个大问题。在这种情况下,您可以调整模型的超参数以最大程度地减少代价最高的错误。 到目前为止,我们所看到的模型都将数字数组作为输入。换句话说,每个输入示例都表示为一个简单的数字列表,其长度是固定的,并且元素的顺序无关紧要,只要它们对于馈入模型的所有示例都是一致的即可。虽然这种类型的模型涵盖了重要的和实用的机器学习问题的很大一部分,但它远非唯一。在接下来的章节中,我们将介绍更复杂的输入数据类型,包括图像和序列。在第 4 章中,我们将从图像开始,图像是一种无处不在且用途广泛的输入数据,已针对其开发了强大的神经网络结构,以将机器学习模型的准确性推向超人的水平。
← 3.2 非线性:分类模型 2.4 总结 →
