3.1 非线性：它是什么，有什么用

让我们从上一章的“波士顿住房”示例中选择我们停下来的地方。使用单个密集层，您会看到训练有素的模型，这些模型会带来大约 5k 美元的偏差。我们可以做得更好吗？答案是肯定的。为了给波士顿住房数据提供更好的模型，我们在其中添加了一个更高的密度层，如下面的代码清单所示。

清单 3.1 限定解决波士顿房屋问题有两层神经网络

export function multiLayerPerceptronRegressionModel1Hidden() {
   const model = tf.sequential();
   model.add(tf.layers.dense({
     inputShape: [bostonData.numFeatures],
     units: 50,
     activation: 'sigmoid',
     kernelInitializer: 'leCunNormal'  #A:
   }));  #B:
   model.add(tf.layers.dense({units: 1}));

   model.summary();  #C:
   return model;
 };

要查看该模型的运行情况，请首先运行第 2 章中提到的“ yarn && yarn watch”命令。打开网页后，在 UI 中单击“ Train Neural Network Regressor（1 hidden layer）”按钮以进行操作，开始训练模型。 该模型是一个两层网络。第一层是具有 50 个单位的致密层。它还配置为具有自定义激活和 kernel 初始化程序，我们将在第 3.1.2 节中进行讨论。该层是一个隐藏层，因为不能从模型外部直接看到其输出。第二层是具有默认激活（“线性”激活）的密集层，在结构上与第二章纯线性模型中使用的层相同。该层是输出层，其输出便是最终输出，这里的输出是模型 predict()方法返回的结果。您可能已经注意到，代码中的函数名称将模型称为“多层感知器”（MLP）。这是一个经常使用的术语，描述了以下神经网络：1）具有简单拓扑结构且不循环（即所谓的前馈神经网络），2）则具有至少一个隐藏层。您在本章中看到的所有模型都符合此定义。

上面清单中的 model.summary ()是一个诊断/报告工具，可将 TensorFlow.js 模型的拓扑打印到控制台中。这是上面的两层模型生成的：

图层（类型）	输出形状	参数＃
density_Dense1（Dense）	[null，50]	650
density_Dense2（Dense）	[null，1]	51

总参数：701 可训练的参数：701 不可训练参数：0 报告中的关键信息包括：

• 图层的名称/类型（第一列）
• 对于每一行，都包括输出形状（第二列）。其中包含的 null，表示未确定且可变的大小。
• 每层的第三列参数是构成层的系数和。例如，在此示例中，第一密集层包含两个系数：形状为[12，50]的 kernel 和形状为[50]的 bias，从而有 12 * 50 + 50 = 650 个参数。
• 在结果的底部，打印了模型参数的总数，细分了可训练的参数和不可训练的参数。到目前为止，我们已经看到的模型仅包含可训练的参数，这些属于在调用 tf.Model.fit ()时可更新的模型参数。在第 5 章中讨论转移学习和模型微调时，我们将讨论不可训练的参数。

下面显示了第 2 章中纯线性模型的 model.summary ()输出。两层模型与线性模型的参数相比，约多出 54 倍。大多数附加参数都来自添加的隐藏层。

图层（类型）	输出形状	参数＃
density_Dense3（Dense）	[null，1]	13

总参数：13 可训练的参数：13 不可训练参数：0

由于两层模型包含更多的层和参数，因此其训练和推理会消耗更多的计算资源和时间。增加的成本会增加准确性吗？当我们训练该模型 200 次时，测试集的最终均方误差落在 14-15（由于初始化的随机性而导致的可变性）范围内，线性模型的测试集的损失约为 25。我们的新模型的错误估计在 3,700 美元-3,900 美元，而纯线性的错误估计大约为 5,000 美元。因此，这是一项改进。

3.1.1 神经网络的非线性模型

图 3.1 为 Boston Housing 数据集创建的线性回归模型（A ）和两层神经网络（B ）的示意图。为更清晰的比较，B 中我们将输入要素的数量从 12 个减少到 3 个，并将隐藏层的单位从 50 个减少到了 5 个，每个模型只有一个输出单元，此类模型求解的是单变量（one-target-number）回归问题。B 说明了模型隐藏层的非线性（Sigmoid）激活。

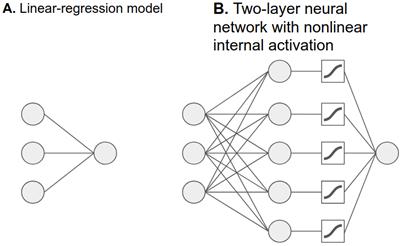
为什么准确度会提高？如上面的图 3.1 所示，关键是增加了模型的复杂性。首先，多加了一层神经元，即隐藏层。其次，隐藏层包含一个非线性激活函数（如代码中的“activation：'sigmoid'”），该函数可由图 3.1B 中的方框表示。激活函数[49]是逐个元素的转换。sigmoid 函数是非线性“压缩”，从某种意义上说，它会将-Infinity 到+ Infinity 的所有实数值“压缩”到一个较小的范围（此为 0 到+1）。其数学公式和曲线图如图 3.2 所示。以隐藏的密集层为例：假设矩阵相乘和相加的结果是带有以下随机值数组的 2D 张量，即

[[1.0]，[0.5]，…，[0.0]]

然后通过在 50 个元素的每个元素上调用 sigmoid（S）函数来获得密集层的最终输出，得到：

[[ S（1.0）]，[S（0.5）]，...，[S（0.0）] = [[0.731]，[0.622]，...，[0.0]]。

图 3.2 深层神经网络的两个常用非线性激活函数。左：sigmoid 函数：S（x）= 1 /（1 + e ^ -x）。右：relu 函数：relu （x）= {0 ：x <0，x ：x > = 0}。

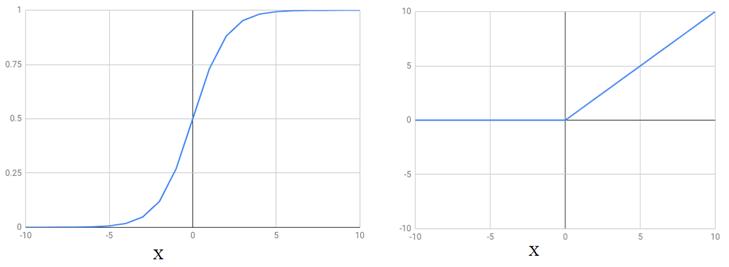
为什么将此函数称为“非线性”？直观地讲，函数的图不是直线。例如，sigmoid 是曲线（图 3.2，左图），relu 是两个线段的串联（图 3.2，右图）。虽然 sigmoid 和 Relu 是非线性的，但是它们在每个点上都是光滑且可微的，这使得在其函数上可以执行反向传播[50]。如果没有此特性，将无法使用包含此激活的图层来训练模型。 除了 sigmoid 函数外，深度学习中还经常使用其他一些类型的可微分非线性函数。这些包括整流线性（或 relu ）和双曲正切（或 tanh）函数。在后续示例中，我们将对其进行详细描述。

3.1.1.1 非线性模型和模型容量

为什么非线性会提高模型的准确性？非线性函数能够表示更多种类的输入输出关系。现实世界中的许多关系都是近似线性的，例如我们在上一章中看到的下载时间问题。但其他许多却不是，比如考虑一个人的身高和他/她的年龄之间的关系，高度仅随着年龄的增长而大致线性变化，直到某个点弯曲并达到平稳。再举一个例子，房价只有犯罪率在一定范围内时，才随着其呈负向变化。在上一章中，纯线性模型无法准确地对此类型的关系进行建模，而 sigmoid 非线性则更适合。当然，犯罪率-房价关系更像是一个倒置的（即下降的）函数。

但是，非线性（例如 Sigmoid）代替线性激活，是否便失去了训练学习中线性关系的考虑？当然，答案是否定的。这是因为 sigmoid 函数的一部分（即靠近中心的部分）非常接近于一条直线。其他常用的非线性激活，例如 tanh 和 relu ，也包含线性或接近线性的部分。如果输入的某些元素与输出的某些元素之间的关系近似线性，则对于具有非线性激活的致密层来说，完全有可能利用激活函数的近线性部分学习相应的权重和偏差。因此，在致密层上添加非线性激活会得到更精确的输入-输出关系。

此外，非线性函数与线性函数的不同之处在于，级联非线性函数会导致更丰富的非线性函数集。在此，“级联”是指将一个函数的输出作为输入传递给另一函数。假设有两个线性函数，

f（x）= k1 * x + b1 和

g（x）= k2 * x + b2

级联这两个函数等于定义一个新函数 h：

h（x）= g（f（x））= k2 （k1 _ x + b1）+ b2 =（k2 _ k1） x +（k2 * b1 + b2）

如您所见，h ()仍然是线性函数。它与 f()和 g()具有不同的内核（即斜率）和偏差（即截距）。斜率现在为（k2 _ k1），偏差为（k2 _ b1 + b2）。级联任意数量的线性函数总是会产生线性函数。

图 3.3 级联线性函数（顶部）和非线性函数（底部）。级联线性函数始终会得到线性函数。级联非线性函数（例如本例中的 relu ）得到具有新颖形状的非线性函数，例如本例中的“下移”函数。这说明了为什么非线性激活及其在神经网络中的级联会得到增强的表示能力（即容量）

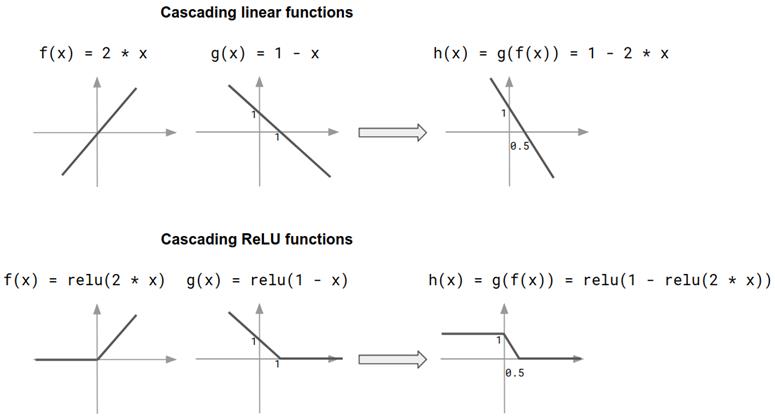
参考经常使用的非线性激活函数：relu 。在图 3.3 的底部，我们说明了使用线性缩放级联两个 relu 函数时发生的情况。通过级联两个 relu 函数，我们得到了一个看起来根本不像 relu 的函数。它具有新的形状（“向下倾斜，两侧为平坦部分”。）将阶跃函数与其他 relu 函数进一步层叠将提供更多的函数集，例如“ window”函数，由多个窗口组成的函数，将窗口堆叠在更宽的窗口顶部的函数等（图 3.3 中未显示）。可以通过级联非线性，例如 relu（最常用的激活函数其中之一）来创建功能范围非常丰富的函数形状，但这与神经网络有什么关系？好吧，实质上，神经网络就是级联函数。神经网络的每一层都可以看作是一个函数，而各层的堆叠相当于将这些函数级联形成更复杂的函数，即神经网络本身。这就是为什么包括非线性激活函数会增加模型的输入输出关系范围的原因。这也使您直观地了解了“添加更多层到深度神经网络”这一常用技巧，以及为什么这种方法经常（但并非总是如此）得到更好的来拟合数据集的模型。

机器学习模型能够学习的输入输出关系的范围通常称为模型的能力。从关于非线性讨论中，我们可以看到，与线性回归相比，具有隐藏层和非线性激活函数的神经网络具有更大的容量。这就解释了为什么与线性回归模型相比，我们的两层网络可以实现更高的测试精度。 您可能会问：由于级联的非线性激活函数会导致更大的容量（例如，图 3.3 的底部），我们是否可以通过向神经网络添加更多隐藏层来获得更好的波士顿住房问题模型？请参见下面的代码摘录。

清单 3.2 限定用于波士顿房屋问题的三层神经网络

export function multiLayerPerceptronRegressionModel2Hidden() {
  const model = tf.sequential();
  model.add(
    tf.layers.dense({
      inputShape: [bostonData.numFeatures],
      units: 50,
      activation: 'sigmoid',
      kernelInitializer: 'leCunNormal'
    })
  ); // ← Adds the first hidden layer.
  model.add(
    tf.layers.dense({
      units: 50,
      activation: 'sigmoid',
      kernelInitializer: 'leCunNormal'
    })
  ); // ← Adds another hidden layer.
  model.add(tf.layers.dense({ units: 1 }));

  model.summary(); // ← Prints a text summary of the model’s topology.
  return model;
}

在 summary()打印输出中，您会看到该模型包含三层，即比清单 3.1 中的模型多一层。与两层模型的 701 个参数相比，它还具有更大的参数：3251。多出来的 2550 参数是由于包含了第二个隐藏层，该第二个隐藏层由形状为[50，50]的 kernel 和形状为[50]的 bias 组成。 重复多次模型训练，我们可以大致了解三层网络的最终测试集（即评估）MSE 的范围，即大约 10.8-13.4。对比两层网络（$ 3,700-$ 3,900 USD）的估计，它具有更小的错误估计 $ 3,280-$ 3,660 USD。因此，我们通过添加非线性隐藏层提高了模型的容量，也提高了模型的预测精度。

3.1.1.2 堆叠层无需非线性的谬误

了解非线性激活对 Boston Housing 模型影响的另一种方法是将其从模型中删除。下面的代码清单 3.3 与代码清单 3.1 相同，只是指定 sigmoid 激活函数的行被注释掉了。删除自定义激活将使图层具有默认的线性激活。模型的其他方面，包括层数和权重参数，都不会改变。

清单 3.3 从清单 3.1 中删除两层神经网络的非线性激活

export function multiLayerPerceptronRegressionModel1Hidden() {
   const model = tf.sequential();
   model.add(tf.layers.dense({
     inputShape: [bostonData.numFeatures],
     units: 50,
     #Activation: 'sigmoid',  // ← Disables the nonlinear activation function.
     kernelInitializer: 'leCunNormal'
   }));
   model.add(tf.layers.dense({units: 1}));

   model.summary();
   return model;
 };

这种变化如何影响模型的学习？您可以通过再次单击 UI 中的“Train Neural Network Regressor (1 hidden layer)”按钮来找到答案，测试中的均方误差上升到约 25，而原来的为 14-15。换句话说，没有 sigmoid 激活的两层模型的性能与单层线性回归的性能大致相同！

图 3.4 比较使用 sigmoid 激活（A）和不使用 sigmoid 激活（B）的训练结果。可以看出，不使用 sigmoid 会导致训练，验证和评估集的最终损失值更高（该水平与之前的纯线性模型相当），而损失曲线则较平滑。两图之间的 y 轴比例不同。

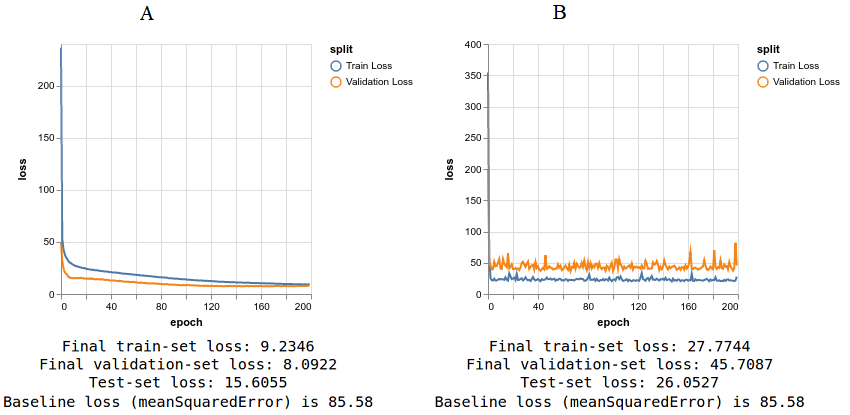
这证实了我们关于级联线性函数的推理。通过消除第一层的非线性激活，我们最终得到一个模型，该模型是两个线性函数的级联。如前所述，其结果是另一个线性函数，而模型的容量没有任何增加。因此，毫不奇怪，我们最终获得的精度与线性模型相同。这在构建多层神经网络时，请确保在隐藏层中包括非线性激活。如果不这样做的结果便是浪费计算资源和时间，从而使得数值不稳定。稍后我们将看到，这不仅适用于密集层，还适用于其他层类型，例如卷积层。

3.1.1.3 非线性与模型可解释性

在第 2 章中，我们显示了一旦在 Boston Housing 数据集上训练了线性模型，便可以检查其权重并以合理有意义的方式解释其各个参数。例如，与“每个住宅的平均房间数”的特征相对应的权重为正值，与“犯罪率”的特征相对应的权重为负值。这些权重的符号反映了房价与各个特征之间预期的正/负关系。它们的大小也暗示了模型分配给各种功能的相对重要性。鉴于您刚刚在本章中学到的知识，一个问题是：对于包含一个或多个隐藏层的非线性模型，是否仍然有可能对其权重进行可理解且直观的解释？

在非线性模型和线性模型之间，访问权重值的 API 完全相同：您只需在模型对象或其组成层对象上使用 getWeights ()方法。以清单 3.1 中的多层感知器（MLP）为例，您可以在模型训练完成后（即在 model.fit ()调用之后）插入以下行：

model.layers[0].getWeights()[0].print();

该行显示第一层（即隐藏层）的 kernel。这是模型中的四个系数之一，其他三个是隐藏层的 bias 和输出层的 kerenel 和 bias。请参见下面的示例，它的大小比我们在打印线性模型的 kernel 时看到的大。

Tensor
     [[-0.5701274, -0.1643915, -0.0009151, ..., 0.1051488 , 0.313205  , -0.3253246],
      [-0.4400523, -0.0081632, -0.2673715, ..., -0.0457693, 0.1735748 , 0.0864024 ],
      [0.6294659 , 0.1240944 , -0.2472516, ..., -0.0732981, 0.2181769 , 0.1706504 ],
      [0.9084488 , 0.0130388 , -0.3142847, ..., -0.3966505, 0.4063887 , 0.2205501 ],
      [0.431214  , -0.5040522, 0.1784604 , ..., -0.018663 , 0.3022115 , -0.1997144],
      [-0.9726604, -0.173905 , 0.8167523 , ..., 1.0440758 , -0.0406454, -0.4347956],
      [-0.2426955, 0.3274118 , -0.3496988, ..., -0.1951355, 0.5623314 , 0.2339328 ],
      [-1.6335299, -1.1270424, 0.618491  , ..., 0.5806215 , -0.0868887, -0.4149215],
      [-0.1577617, 0.4981289 , -0.1368523, ..., 0.1700188 , 0.3636355 , -0.0784487],
      [-0.5824679, -0.1883982, -0.4883655, ..., -0.7185445, 0.0026836 , -0.0549298],
      [-0.6993552, -0.1317919, -0.4666585, ..., -0.6055267, 0.2831602 , -0.2487895],
      [0.0448515 , -0.6925298, 0.4945385 , ..., 0.5185578 , -0.3133179, -0.0241681]]

这是因为隐藏层由 50 个单位组成，大小为[18，50]。与线性模型内核中的 12 +1 = 13 个参数相比，该内核具有 900 个单独的权重参数。可以给每个单独的参数赋予一种含义吗？答案是否定的。这是因为隐藏层的 50 个输出中的任何一个都没有易于识别的含义。这些是创建的高维空间的维，以便模型可以学习其中的非线性关系。人类的头脑不是很擅长跟踪此类高维空间中的非线性关系。通常，很难用几句话来描述每个隐藏层的参数做什么，或者很难解释它对深度神经网络的最终预测做出哪些贡献。 另外，这里的模型只有一个隐藏层。当存在多个彼此叠加的隐藏层时（如清单 3.2 定义的模型中的情况），这种关系变得更加晦涩难于描述。尽管人们正在努力寻找更好的方法来解释深度神经网络隐藏层的含义[51]，并且某些类型的模型取得了一些进展[52]，但深度神经网络与浅层神经网络和某些类型的非神经网络机器学习模型（例如决策树）相比很难进行解释。适用较深的模型替换较浅的模型，实质上是在用可解释性换取更大的模型容量。

3.1.2 超参数和超参数优化

我们在代码清单 3.1 和 3.2 中对隐藏层的讨论一直集中在非线性激活（“ sigmoid”）上。但是，此层的其他配置参数对于确保此模型获得良好的训练结果也很重要。这些包括单元数（50）和 kernel 的' leCunNormal '初始化。后者是一种根据输入大小生成内核初始值的特殊方法。它与默认的内核初始化程序（即 glorotNormal ）不同。glorotNormal 使用输入和输出的大小。那么问题是：为什么要使用此自定义内核初始化而不是默认的？为什么要使用 50 个单位（而不是 30 个单位）？答案是：这些是通过反复尝试各种参数组合，以求获得最佳模型质量而选取的。

单元数，内核初始化和激活相关的参数都是模型的超参数。“超参数”：这些参数与模型的权重参数不同，权重参数在训练过程中通过反向传播自动更新（即，调用 Model.fit ()）。一旦为模型选择了超参数，它们就不会在训练过程中改变。他们通常确定参数的数量和大小（例如 units），参数的初始值（例如 kernelInitializer ）以及在训练期间如何更新它们（例如考虑传递 Model.compile ()的优化器字段）。因此，它们的级别高于权重参数。因此，称为“超参数”。

除了层的大小和参数初始化的类型外，模型及其训练还有许多其他类型的超参数，例如：

• 清单 3.1 和 3.2 中的模型中密集层的数量
• 密集层 kernel 使用哪种类型的初始化
• 是否使用权重正则化（请参阅第 8.1 节），如果是，正则化因子是多少
• 是否包括任何 dropout 层（请参见第 4.3.2 节），如果包含，则 dropout 率是多少
• 用于训练的优化器的类型的选择（‘egd’vs‘adam’，详见信息框 3.1）
• 需要多少次来训练模型
• 优化器的学习率
• 是否应随着训练的进行逐渐降低优化器的学习率，如果是，应以什么速率降低
• 训练的批量大小 上面列出的最后五个示例有些特殊，因为它们与模型本身的体系结构无关。它们是模型训练过程的配置。但是，它们会影响训练的结果，因此被视为超参数。对于由更多样化类型的层（卷积和复发性层，参见第 4，5 和 9 章），还有更潜在的可调谐的超参数。因此，为什么即使是简单的深度学习模型也可能具有数十个可调超参数。 选择良好的超参数值的过程称为超参数优化或超参数调整。超参数优化的目标是找到一组参数，使训练后的验证损失最小。但是当前没有确定的算法可以在给定数据集和所涉及的机器学习任务的情况下确定最佳超参数。困难在于：许多超参数是离散的，因此验证损失值就它们而言是不可微分的。密集层 units 的数值和模型中致密层数都是整数; 优化器的类型是一个分类参数。即使对于连续且验证损失可与之相关的超参数（例如正则化因子），在训练过程中计算上也过于昂贵，因此超参数空间中的梯度下降法得到参数并不可行。当然超参数优化仍然是研究的活跃领域，深度学习的从业者应关注这一领域。

鉴于缺乏用于超参数优化的标准现成方法或工具，深度学习从业人员经常使用以下方法：

首先，如果手头的问题类似于经过充分研究的问题，则可以从对问题应用类似的模型开始，并“继承”超参数。随后，您可以在该起点周围相对较小的超参数空间中进行搜索。

其次，具有足够经验的从业者可能对给定问题会对合理的超参数进行有根据的猜测。即使这样的主观选择几乎从来都不是最佳选择，但是这是不错的起点，并且可以在后续进行微调。

第三，对于只有少量超参数要优化（例如，少于四个）的情况，可以使用网格搜索，即，在多个超参数组合上进行详尽的迭代，记录验证损失，并采用产生最低验证损失的超参数组合。例如，假设要调整的仅有两个超参数是：a）密集层中的单位数量和 b）学习率，那么您可以选择一组单位（例如{10、20、50、100、200} ）和一组学习率（例如{1e-5、1e-4、1e-3、1e-2}）并进行两组交叉运算，从而得出总共 5 * 4 = 20 个超参数组合搜索。如果您要自己实现网格搜索，则伪代码可能如下所示：

清单 3.4 用于简单超参数网格搜索的伪代码

function hyperparameterGridSearch():
   for units of [10, 20, 50, 100, 200]:
     for learningRate  of [1e-5, 1e-4, 1e-3, 1e-32]:
        创建模型中的密集层是用单元 `units`中的数据
        训练模型的优化器使用 `learningRate`中的数据
        最终验证损失 为validationLoss
        if 最终验证损失 < 最小验证损失
          最终验证损失 =  最终验证损失
          最优的单元数 = units
          最优的学习率= learningRate

   return [bestUnits, bestLearningRate]

如何选择这些超参数的范围？深度学习无法提供答案。这些范围通常基于深度学习从业者的经验和直觉，也可能受到计算资源的限制。例如，具有太多单元的密集层可能导致模型在推理期间太慢而无法训练和运行。 通常，如果要优化大量的超参数，在计算上会过于昂贵以至于无法成倍增加超参数组合数量。在这种情况下，可以使用比网格搜索更复杂的方法，例如随机搜索[53]和贝叶斯[54]方法。对于这些方法，存在一个开源的第三方库 hpjs 。本章末尾的练习为您提供了动手实践的机会。