2.1 示例 1：使用 TensorFlow.js 预测下载的持续时间

我们将构建一个最小神经网络，根据下载文件大小，利用 TensorFlow.js（TFJS）库预测下载时间。除非您已经有使用 TFJS 或类似库的经验，否则您不会立即理解第一个示例的所有内容，这很好。这里介绍的每一个主题都将在接下来的章节中详细介绍，所以不要担心某些部分在你看来是模糊的！我们将从编写一个接受文件大小作为输入的短程序开始，并输出下载文件的预计时间。

2.1.1 概况：预测

当你第一次学习机器学习系统时，你可能会被各种各样的新概念和术语吓倒。因此，首先查看整个工作流是有帮助的。这个例子的概要如下图所示，我们将在本书的例子中重复看到这个模式。

图 2.1 第一个示例，“下载时间预测”系统中涉及的主要步骤概述。

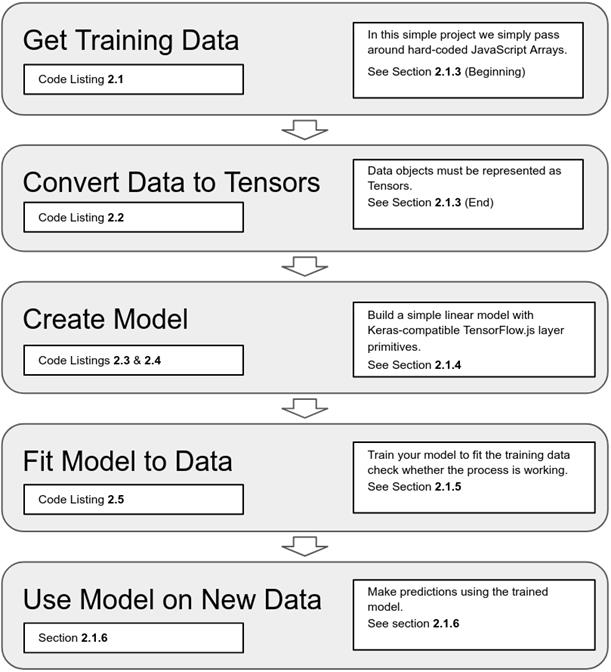
首先，我们将访问我们的训练数据。在机器学习中，数据可以从磁盘读取、通过网络下载、生成或是简单地硬编码。在这个例子中，我们采用了最后一种方法，因为它很方便，而且我们只处理少量数据。接下来，我们将数据转换成张量，这样它们就可以被输入到我们的模型中。下一步是创建一个模型，正如我们在第一章中看到的，它类似于设计一个合适的可训练函数：一个将输入数据映射到我们试图预测事物的函数。在这种情况下，输入数据和预测目标都是数字。一旦我们的模型和数据可用，我们将对模型进行训练，同时关注其输出情况。最后，我们将使用经过训练的模型对我们尚未看到的数据进行预测，并测量模型的准确性。 我们将通过复制-粘贴可运行的代码片段，以及对理论和工具的解释，来完成每个阶段。

2.1.2 关于代码列表和控制台交互的说明

本书中的代码将以两种格式呈现。 第一种格式是代码列表，它显示了您可以在引用的代码存储库中找到的结构代码。每个列表都显示在一个框中，包括一个标题和一个数字。例如，下面清单 2.1 中的示例包含一个非常简短的 HTML 代码片段，您可以将其逐字复制到文件中，例如，在您的计算机上，尽管它在/tmp/tmp.html，但是在 web 浏览器中打开file：///tmp/tmp.html。

代码的第二种格式是控制台交互。这些非正式的代码块旨在 JavaScript REPL[38]上的示例交互，例如浏览器的 JavaScript 控制台（Cmd-Opt-J, Ctrl+Shift+J、或 Chrome 中的 F12，但您的浏览器/操作系统可能不同）。控制台交互在前面用大于号表示，就像我们在 Chrome 或 Firefox 中看到的那样，它们的输出显示在下一行。例如，下面的交互创建一个数组并打印值。您在 JavaScript 控制台上看到的输出可能略有不同，但要点应该是相同的。

> let a = ['hello', 'world', 2 * 1009]
> a;
 (3) ["hello", "world", 2018]

从本书中的代码中测试、运行和学习的最佳方法是克隆引用的存储库，然后使用它们。在本书的开发过程中，我们经常会使用一个简单的交互式共享存储库“CodePen”（http://CodePen.io）。例如，清单2.1可以在codepen.io/tfjs-book/pen/VEVMbx上实现。当您导航到“CodePen”页面时，它会自动运行。您应该能够看到打印到控制台的输出。单击左下角的“控制台”打开控制台。如果“CodePen”没有自动运行，尝试做一些小更改，比如在结尾添加一个空格，以启动它。

此部分可在 CodePen 代码集 CodePen.io/collection/Xzwavm/中找到。CodePen 在只有一个 JS 文件的地方工作得很好，但是在后面的示例中将更大、更结构化的示例就需要保存在 GitHub 存储库中。对于本例，我们建议阅读本节内容，然后按顺序执行相关的“CodePen”。

2.1.3 创建和格式化数据

只要给定它的大小（以 MB 为单位），我们就可以估计出在给定的机器上下载一个文件需要多长时间。我们将首先使用预先创建的数据集，但是，如果您有兴趣，可以创建一个类似的数据集，对您自己系统的网络统计数据进行建模。

<script src='https://cdn.jsdelivr.net/npm/@tensorflow/tfjs@latest'></script>
 <script>
 const trainData = {
   sizeMB:  [0.080, 9.000, 0.001, 0.100, 8.000, 5.000, 0.100, 6.000, 0.050, 0.500,
             0.002, 2.000, 0.005, 10.00, 0.010, 7.000, 6.000, 5.000, 1.000, 1.000],
   timeSec: [0.135, 0.739, 0.067, 0.126, 0.646, 0.435, 0.069, 0.497, 0.068, 0.116,
             0.070, 0.289, 0.076, 0.744, 0.083, 0.560, 0.480, 0.399, 0.153, 0.149]
 };
 const testData = {
   sizeMB:  [5.000, 0.200, 0.001, 9.000, 0.002, 0.020, 0.008, 4.000, 0.001, 1.000,
             0.005, 0.080, 0.800, 0.200, 0.050, 7.000, 0.005, 0.002, 8.000, 0.008],
   timeSec: [0.425, 0.098, 0.052, 0.686, 0.066, 0.078, 0.070, 0.375, 0.058, 0.136,
             0.052, 0.063, 0.183, 0.087, 0.066, 0.558, 0.066, 0.068, 0.610, 0.057]
 };
 </script>

这里介绍了如何使用@latest 后缀加载 tfjs 库的最新版本（在编写本文时，此代码使用 tfjs 0.13.5 运行）。稍后我们将更详细地介绍将 TFJS 导入到应用程序中的不同方法，但需要提前引用<script>。第一个script>加载 TensorFlow 包并定义成tf，该符号提供了一种引用TensorFlow中名称的方法。例如，引用tf.add()是 TensorFlow add 的操作，该操作添加两个张量。接下来，通过加载上述的 tfjs 脚本，tf 在全局中便可用。

上面的清单创建了两个常量，trainData 和 testData，每个常量表示下载一个文件花费的时间（timeSec）和该文件的大小（sizeMB）的 20 个示例。sizeMB 中的元素和 timeSec 中的元素有一一对应的关系。例如，训练数据中的第一个元素有 0.080 MB，下载该文件需要 0.135 秒，即第一个元素的 timeSec，以此类推。我们在这个例子中只要给出 sizeMB，那就能估计出 timeSec。在第一个例子中，我们通过在代码中硬编码直接创建数据。这种方法对于这个简单的例子来说是方便的，但是当数据集的大小增加时，它会变得非常笨拙。之后的例子将说明介绍从外部存储器或通过网络传输数据得到输入数据。

回到数据上。从下面的图表中，我们可以根据文件大小和下载时间对互相进行预测。现实生活中的数据是复杂的，但是在这个例子中，我们应该能够对给定文件大小的持续时间做出很好的线性估计。根据判断，当文件大小为 0 时，持续时间应该为 0.1 秒左右，然后每增加一个 MB，持续时间就增加 0.07 秒左右。

图 2.2 测量的下载持续时间与文件大小。如果您对如何创建这样的绘图感兴趣，那么代码将列在 code pen CodePen.io/tfjs-book/pen/dgQVze 中

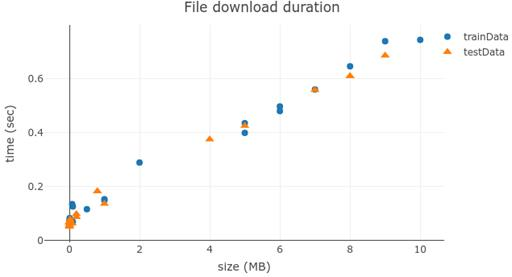
回顾第一章，每个输入输出对有时被称为一个例子。输出通常称为目标，而输入的元素通常称为特征。在我们的例子中，40 个例子中的每一个都有一个特征，比如代表大小的 sizeMB，和代表时间的数字 timeSec。 在清单 2.1 中，您可能注意到数据被分成两个子集，即训练数据和测试数据。训练数据是训练集合。它包含模型将要学习的示例。测试数据是测试集。我们将使用它来判断模型在训练完成后的训练效果。如果我们使用完全相同的数据进行训练和测试，就像在看到答案后又进行测试一样。在最极端的情况下，该模型理论上可以记住训练数据中每个数据的值——这看上去不是一个很好的算法。此结果不能很好地判断训练模型的优劣，因为之后输入特性的值一般不与模型所训练的值完全相同。

本文的工作流程总结如下：首先在训练数据上拟合神经网络，对给定的数据进行准确预测。最后，我们将使用网络输入测试数据的 sizeMB，来预测 timeSec。但首先，我们必须将这些数据转换成 TFJS 能够理解的格式，这是我们使用张量的第一个例子。清单 2.2 中的代码显示了您将在本书中看到的tf.*名称空间下函数的第一次使用。这里我们展示了存储在原始 JavaScript 数据结构中的数据转换为张量的方法。尽管用法非常简单，但是那些希望在这些 api 中更进一步的读者应该阅读本书末尾的附录 A4，它不仅涵盖了像 tf.tensor2d()`等创建张量的函数，还包括执行操作转换和组合张量的函数，以及如何按惯例打包成张量的常见（如图像的和视频的）数据类型。我们并没有深入研究主文本中的低级 API，因为这些材料有些枯燥，没有与特定的示例问题联系在一起。

清单 2.2 将数据转换成张量（来自 CodePen 2-b）

const trainTensors = {
   sizeMB: tf.tensor2d(trainData.sizeMB, [20, 1]),  #A:
   timeSec: tf.tensor2d(trainData.timeSec, [20, 1])
 };
 const testTensors = {
   sizeMB: tf.tensor2d(testData.sizeMB, [20, 1]),
   timeSec: tf.tensor2d(testData.timeSec, [20, 1])
 };

一般来说，目前所有的机器学习系统都使用张量作为基本的数据结构。其中张量是基本要素，因此 TensorFlow 和 TensorFlow.js 也以它们命名。第一章的快速回顾：

张量是数据的容器-几乎总是数值数据。所以它可以被看作是数字的容器。您可能已经熟悉了向量和矩阵，它们分别是一维张量和二维张量。张量是矩阵到任意维数的推广。维度的数量和每个维度的大小称为张量的形状。例如，一个 3 x 4 的矩阵是具有形状[3,4]的张量。长度为 10 的向量是具有形状的一维张量[10]。 在张量的上下文中，维数通常称为轴。在 TensorFlow.js 中，tensor 是一种常见的表示形式，无论是在 CPU、GPU 还是其他硬件上，它允许组件之间进行通信和工作。随着需求的增加，我们将有更多关于张量及其常见用例的讨论，但是现在让我们继续我们的预测。

2.1.4 定义简单模型

在深度学习的背景下，从输入特征到目标的函数称为模型。模型函数获取特征、运行计算并生成预测。我们在这里建立的模型是一个以文件大小作为输入和输出持续时间的函数（见图 2.2）。在深度学习的术语中，有时我们使用网络作为模型的同义词。我们的第一个模型将是线性回归。

在机器学习的背景下，回归意味着模型将输出实值数字并尝试匹配训练目标，而分类则从一组选项中输出选择。在回归任务中，输出离目标较近的数字的模型比输出离目标较远的数字的模型要好。如果我们的模型预测一个 1MB 文件大约需要 0.15 秒，那么（如图 2.2 所示）比我们的模型预测一个 1MB 文件大约需要 600 秒要好。

线性回归是一种特殊的回归类型，其中输出作为输入的函数，可以表示为一条直线（或者类比地，当存在多个输入特征时，可以表示为高维空间中的平面）。模型的一个重要特性是它们是可调的。这意味着可以调整输入输出计算。我们使用此属性来优化模型以更好地“拟合”数据。在线性情况下，模型的输入输出关系总是一条直线，但我们可以调整斜率和 y 截距。 让我们建立我们的第一个网络：

清单 2.3 构造一个线性回归模型（来自 CodePen 2-c）

const model = tf.sequential();
model.add(tf.layers.dense({ inputShape: [1], units: 1 }));

神经网络的核心组成部分是层，这是数据处理模块，你可以把它看作是一个从张量到张量的可调函数。在这里，我们的网络由一层组成。该层对输入张量的形状有约束为[1q]。这意味着该层期望输入的形式是一个只有一个值的一维张量。对于每个示例，密集层的输出始终是一维张量，但该维度的大小由单元配置参数控制。在这种情况下，我们只需要一个输出数字，因为我们正试图准确地预测一个数字，即 timeSec。

密集层是一个在每个输入和每个输出可调的倍增部分。由于只有一个输入和一个输出，这个模型是一个简单的线性方程y = m * x + b。层内部的 m 是 kernel 和 b 是偏差，如图 2.3 所示。因此在本例中，我们为输入（sizeMB）和输出（timeSec）之间的关系构造了一个线性模型。timeSec = kernel * sizeMB + bias

这个方程式有四项。就模型训练而言，其中受训练数据影响的两个参数是固定的:（sizeMB）和（timeSec）（见清单 2.1）。另外两个项，即 m 和偏差 b，是模型的参数。它们的值是在创建模型时是随机选择的。这些随机值不能很好地预测下载持续时间。为了进行更准确的预测，我们必须通过模型从数据中学习来寻找更好的 kernel 值和偏差值。这个搜索就是训练过程。

为了找到一个好的 kernel 值和偏差值（统称为“系数”），我们需要两件事：

• 一种测量方法，使用系数进行反馈。
• 一种更新系数值的方法，根据上面提到的度量，下次会比现在做得更好。

图 2.3 简单线性回归模型的图解。模型只有一层。模型的可调参数（或系数）显示在稠密层中。

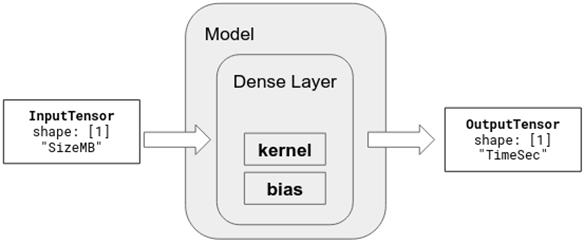
下面便是解决线性回归问题的下一步。为了使网络更好的接受训练，我们需要选择与上面列出的两个必需项相对应的度量和更新方法。这是 TFJS 所称的模型编译步骤的一部分，即：

• 损失函数--误差测量。这是如何在训练数据上测量网络的性能。损失越少越好，当我们训练时，我们应该能够计算出随着时间的推移所造成的损失，并看到误差的下降。如果我们的模型训练了很长一段时间，损失没有减少，这可能意味着我们的模型没有习得去拟合数据。在这本书的过程中，你将学会调试这样的问题。
• 一个优化器--网络根据数据和损失函数更新其系数的算法。 关于 loss 函数和优化器的确切目的，以及如何为它们选择，将在接下来的几章中进行深入的探讨。

清单 2.4 配置训练选项：模型编译（来自 CodePen 2-c）

model.compile({ optimizer: 'sgd', loss: 'meanAbsoluteError' });

在清单 2.4 中，我们在模型上调用 compile 方法，将“ sgd”指定为优化器，将“ meanAbsoluteError”指定为损耗。 “ meanAbsoluteError”表示损失函数，计算预测与目标之间的距离，取其绝对值（使它们全部为正），然后返回这些值的平均值。

meanAbsoluteError = average( absolute(modelOutput - targets) )

例如，给定：

modelOutput = [1.1, 2.2, 3.3, 3.6];
targets = [1.0, 2.0, 3.0, 4.0];

然后，

meanAbsoluteError = average([|1.1 - 1.0|, |2.2 - 2.0|,
                              |3.3 - 3.0|, |3.6 - 4.0|])

                   = average([0.1, 0.2, 0.3, 0.4])

                   = 0.25

如果我们的模型做出了非常糟糕的预测，并且与目标相距甚远，那么 meanAbsoluteError 将会非常大。相反，我们使每个预测完全正确，在这种情况下，模型输出与目标之间的差异将为零，因此损失“ meanAbsoluteError”将为零。

清单 2.4 中的“ sgd”代表随机梯度下降，我们将在下面的 2.2 节中对其进行更多描述，简要地讲，我们将使用微积分来确定应对系数进行哪些调整以减少损失;然后进行调整并重复该过程。 现在，我们的模型已经准备就绪。

2.1.5 在训练数据中进行模型拟合

通过调用模型的fit()方法，可以在 TFJS 中训练模型。我们将在训练数据中进行模型拟合。我们传入sizeKB张量作为输入，并将timeMS张量作为输出。我们还将传入一个带有 epochs 字段的配置对象，该字段指定我们希望对训练数据进行 10 次遍历。在深度学习中，整个训练集的每次迭代都称为一个 epoch。

清单 2.5 线性回归模型拟合

(async function() {
  await model.fit(trainTensors.sizeMB, trainTensors.timeSec, { epochs: 10 });
})();

我们利用了 ES2017 / ES8 的 async / await 功能，以便可以在浏览器中运行时以不阻塞主 UI 线程来使用此 fit()方法。这类似于 JavaScript 中‘异步获取’需要消耗长时间的函数。这里，我们使用“立即调用的异步函数表达式” [39]模式等待 fit 调用完成，然后再继续，但是之后的示例将在后台进行训练，前台线程中会执行其他工作。

一旦模型完成拟合，我们将要查看它是否有效。我们将根据训练期间未使用的数据来评估模型。将测试与训练数据分离（从而避免对测试数据进行训练）的主题将在本书中反复出现。这是机器学习工作流程中的重要组成部分。

> model.evaluate(testTensors.sizeMB, testTensors.timeSec).print();
 Tensor
     0.31778740882873535

模型的评估方法是计算损失函数，并将其应用于提供的示例特征和目标。它与 fit()方法相似，但评估不会更新模型的系数。我们使用 evaluate()来评估测试数据上模型的优劣，以便对模型在将来的应用程序中的表现有所了解。

在这里，我们看到测试数据中的平均损耗约为 0.318。由于默认情况下模型是从随机初始状态训练而来的，因此您将获得不同的值。换句话说，该模型的平均绝对误差接近 0.3 秒。这个好吗？我们可以选定一个常数为平均延迟。让我们看看 TFJS 对张量的数学运算会产生什么样的误差。首先，我们将计算在我们的训练集上的平均下载时间。

> const avgDelaySec = tf.mean(trainData.timeSec);
> avgDelaySec.print();
 Tensor
     0.2950500249862671

接下来，让我们手动计算 meanAbsoluteError。平均绝对误差仅是我们的预测与实际值相差多少的平均值。我们将使用 tf.sub()来计算测试目标与我们的（恒定）预测之间的差异，tf.abs()来获取绝对值，并且然后以 tf.mean 取平均值。

> tf.mean(tf.abs(tf.sub(testData.timeSec, 0.295))).print();
 Tensor

信息框 2.1 张量的链式 API

在 tf 命名的 API 中，有些方法可以使用链式 API 来实现，比如下面的代码和meanAbsoluteError是一致的。

testData.timeSec.sub(0.295).abs().mean().print(); #Chaining API pattern
Tensor
0.22020000219345093 :::

预测的平均误差约为 0.295 秒，其比我们的网络有着更好的估计。这意味着我们模型的准确性甚至比常识的方法还要差！我们可以做得更好吗？我们可能没有经过足够的训练。请记住，在训练过程中，kernel 和 bias 的值会逐步更新。在这种情况下，每个 epoch 都是一个步骤。如果仅针对少数时期（步骤）训练模型，则参数值很难接近最佳值。让我们再训练模型几个周期，然后再次评估。

> model.fit(trainTensors.sizeMB, trainTensors.timeSec, {epochs: 200});

好多了！看来我们以前的模型尚未充分拟合训练数据。现在，我们的估计平均在 0.05 秒以内。比猜测的平均值要精确四倍。在这本书中，我们将提供有关如何避免过度拟合以及更隐蔽的过度拟合问题的指南。

2.1.6 使用训练模型进行预测

好的，不错！因此，现在有了一个可以在给定输入文件大小的情况下准确预测下载时间的模型，但是我们如何使用它呢？答案是模型的预测方法。

> const smallFileMB = 1;
 > const bigFileMB = 100;
 > const hugeFileMB = 10000;
 > model.predict(tf.tensor2d([[smallFileMB], [bigFileMB], [hugeFileMB]])).print();
 Tensor
     [[0.1373825  ],
      [7.2438402  ],
      [717.8896484]]

在这里，我们看到我们的模型预测 10,000 MB 的文件下载将花费大约 718 秒。请注意，我们的训练数据中没有任何接近此大小的示例。通常，将数据外推到训练数据之外是非常冒险的，但是存在一个简单的问题，只要我们不遇到内存缓冲区，I / O 连接等新问题，它是否可能是准确的呢。如果我们可以在此范围内收集更多的训练数据，那就更好了。

我们需要将输入变量包装到适当形状的张量中。在清单 2.3 中，我们将输入形状（即维度）定义为[1]，因此模型期望每个示例都具有该形状。 fit()和 predict()一次可以处理多个示例。为了提供 n 个样本，我们将它们堆叠在一起成为单个输入张量，因此该张量必须具有[n，1]的形状。如果我们忘记了，而是为模型提供了错误形状的张量，那么我们将出现错误，例如以下代码：

> model.predict(tf.tensor1d([smallFileMB, bigFileMB, hugeFileMB])).print();
 Uncaught Error: Error when checking : expected dense_Dense1_input to have 2 dimension(s), but got array with shape [3]

请注意这种形状不匹配的情况，因为这是非常常见的错误！

2.1.7 第一个示例的总结

下图显示了模型的输出（timeSec）与输入（sizeMB）的函数关系，对于模型在过程中的四条线，从 10 次的欠拟合开始，到 200 次收敛

图 2.4 在 10/20/100/200 次循环训练后的线形模型

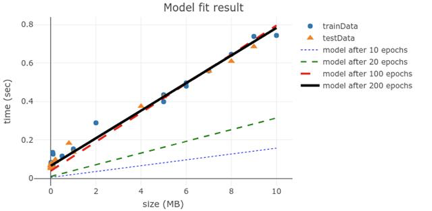
如果您对如何绘制上述数据有兴趣，请访问codepen.io/tfjs-book/pen/VEVMMd。

这就是我们的第一个例子。 您刚刚看到了如何用很少的几行 JavaScript 代码来构建，训练和评估 TFJS 模型。 在下一节中，我们将更深入地研究 model.fit 内部的情况。

清单 2.6 构建，训练和评估 TFJS 模型

const model = tf.sequential([tf.layers.dense({ inputShape: [1], units: 1 })]);
model.compile({ optimizer: 'sgd', loss: 'meanAbsoluteError' });
(async () => await model.fit(trainTensors.sizeMB, trainTensors.timeSec, { epochs: 10 }))();
model.evaluate(testTensors.sizeMB, testTensors.timeSec);
model.predict(tf.tensor2d([[7.8]])).print();