# 2.3 具有多个输入特征的线性回归
在第一个示例中,我们只有一个输入特征 sizeMB ,以及一个可用来预测的目标 timeSec 。更为常见的情况是具有多个输入特征,不确切哪些特征最具有预测性,哪些特征与目标之间的关系松散,仍需要同时使用它们并让算法对其进行分类。在本章中,我们将解决这个更复杂的问题。
到本节末,您将
- 了解如何建立一个可以输入多种特征并从中学习的模型
- 使用 yarn,git 和标准 JS 项目打包来构建和运行带有 ML 的网络应用
- 知道如何规范化数据以稳定学习过程
- 训练时使用 tf.Model.fit()回调来更新 Web UI
# 2.3.1 波士顿房屋价格数据集
波士顿房屋价格数据集[41]收集了 1970 年代后期在马萨诸塞州波士顿及其周边地区收集的 500 条简单的房地产记录,几十年来一直用作介绍性统计数据和机器学习问题的标准数据集。数据集中的每个独立记录都包含波士顿邻域的数字度量,其中包括例如房屋的大小,该区域距离最近的高速公路有多远,该区域是否具有滨水性质等。下面提供了特征的精确排序列表以及每个特征的平均值。
# 表 2.1 波士顿住房数据集的特征
| 指数 | 特征简称 | 特征说明 | 平均值 | 范围(最大-最小) |
|---|---|---|---|---|
| 0 | CRIM | 犯罪率 | 3.62 | 88.9 |
| 1 | ZN | 占地超过 25,000 平方英尺的住宅用地比例 | 11.4 | 100 |
| 2 | INDUS | 城镇非零售营业面积(工业)的比重 | 11.2 | 27.3 |
| 3 | CHAS | 该地区是否毗邻查尔斯河 | 0.0694 | 1 |
| 4 | NOX | 一氧化氮浓度(百万分之一) | 0.555 | 0.49 |
| 5 | RM | 每个住宅的平均房间数 | 6.28 | 5.2 |
| 6 | AGE | 1940 年之前建造的自有住房的部分 | 68.6 | 97.1 |
| 7 | DIS | 到五个波士顿就业中心的加权距离 | 3.80 | 11.0 |
| 8 | RAD | 径向公路通达性指数 | 9.55 | 23.0 |
| 9 | TAX | 每 10,000 美元的税率 | 408 | 524.0 |
| 10 | PTRATIO | 师生比例 | 18.5 | 9.40 |
| 11 | LATAT | 未接受高中教育的在职男性百分比 | 12.7 | 36.2 |
| 12 | MEDV | 拥有住房的中位数价值,单位为$ 1,000 US | 22.5 | 45 |
在本节中,我们将构建,训练和评估一个学习系统,以根据所有输入特征来估计房价的中位数(MEDV )。您可以将其想象为一个根据社区的可测量属性估算房地产价格的系统。因为此问题更大,并且涉及更多问题,所以我们将以工作代码存储库的形式提供解决方案,然后指导您完成该过程。
# 2.3.2 从 GitHub 获取并运行 Boston-housing 项目
由于此问题比下载时间预测示例要大一些,并且涉及更多问题,因此我们将从以工作代码存储库的形式提供解决方案开始,然后指导您完成该过程。如果您已经是 git 工作流程和 npm / yarn 包管理的专家,则可能需要快速浏览此小节。
我们将从在 GitHub [42]中源代码克隆项目存储库开始,以获取项目所需的 HTML,JS 和配置文件的副本。除了最简单的代码托管在 CodePen 上,本书中的所有示例都收集在两个 git 存储库之一中,然后按存储库中的目录分隔。这两个存储库是 tensorflow / tfjs-examples 和 tensorflow / tfjs-models ,它们都托管在 GitHub 上。以下命令将在本地克隆此示例所需的存储库,并将工作目录更改为波士顿住房预测项目。
git clone https://github.com/tensorflow/tfjs-examples.git
cd tfjs-examples/boston-housing
信息框 2.3
本书中使用的示例的基本 JavaScript 项目结构
我们将在本书示例中使用的标准项目结构包括三种重要的文件类型。第一个是 HTML。我们将使用的 HTML 文件主要用作包含一些组件的基本结构。通常,只有一个 html 文件,名为 index.html ,它将包含一些 div 标签,也许一些 UI 元素以及一个源标签,以 JavaScript 代码插入例如 index.js 。
JS 代码通常分为几个文件,以提高良好的可读性和工程样式。在这个波士顿住房项目中,用于更新视觉元素的代码位于 ui.js 中,而用于下载数据的代码位于 data.js 中。两者都是通过 index.js 的 import 语句引用的。
我们将使用的第三个重要文件类型是软件包元数据 package.json 文件,这是 npm [43]软件包管理器。如果您以前从未使用过 npm 或 yarn ,建议您在https://docs.npmjs.com/getting-started/what-is-npm上浏览一下npm“入门”文档,并逐渐熟悉以便能够构建并运行示例代码。我们将使用yarn [44]作为我们的包管理器,但如果 npm 包更适合您的需求,您可以用 npm 来代替。
在存储库中,请注意以下重要文件:
1. index.html :HTML 根文件,提供 DOM 根并调用 JS 脚本。
2. index.js :根文件,用于加载数据,定义模型,训练循环并指定 UI 元素
3. data.js :实现下载和访问 Boston Housing Dataset 所需的数据结构
4. ui.js :用于将 UI 元素连接到动作的 UI 钩的实现。
5. normalization.js 运算方法,例如,从数据中减去平均值
6. package.json :标准的 npm 软件包定义文件,描述了构建和运行此示例所需的依赖项(例如 tfjs!)。
请注意,我们没有遵循将 HTML 文件和 JS 文件放在特定类型的子目录中的标准做法。这种模式虽然是大型存储库的最佳实践,但对于我们在本书中使用的较小示例或您可以在 github.com/tensorflow/tfjs-examples 上找到的较小示例而言,其模糊性更大。
要运行演示,请使用 yarn:yarn && yarn watch
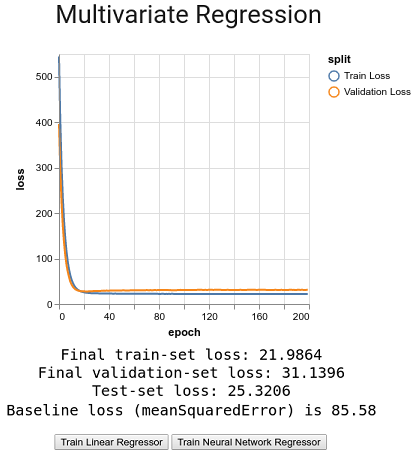
在浏览器中打开一个新标签,指向将运行示例的 localhost 上的端口。如果浏览器没有自动响应,则可以导航到命令行上的 URL 输出。单击标记为“ Train Linear Regressor”的按钮将触发,以建立线性模型并将其拟合到 Boston Housing 数据,并在每个循环训练之后在训练和测试数据集上输出损失的动画图,如图 2.11 所示。
本节的其余部分将详细介绍此波士顿房屋线性回归网络应用演示的构建要点。我们将首先回顾如何收集和处理数据,以便与 TensorFlow.js 一起使用。然后,我们将专注于模型的构建,训练和评估,最后,我们将在网页上展示如何将模型用于实时预测。
# 图 2.11 tfjs-examples 中波士顿住房的线性回归例子
# 2.3.3 访问波士顿住房数据
在清单 2.1 中的第一个项目中,我们将数据硬编码为 JS 数组,并使用 tf.tensor2d 函数将其转换为张量。硬编码对于一些演示很好,但是显然不能扩展到更大的应用程序。通常,JS 开发人员会发现他们的数据以某种序列化格式位于某个 URL(可能是本地)上。例如,可以从以下网址的 Google Cloud 中以 CSV 格式公开和免费获得 Boston Housing 数据:
https://storage.googleapis.com/tfjs-examples/multivariate-linear-regression/data/train-data.csv
https://storage.googleapis.com/tfjs-examples/multivariate-linear-regression/data/train-target.csv
https://storage.googleapis.com/tfjs-examples/multivariate-linear-regression/data/test-data.csv
https://storage.googleapis.com/tfjs-examples/multivariate-linear-regression/data/test-target.csv
通过将样本随机分配到训练和测试部分中,可以对数据进行预分割。⅔ 样品来训练,其余 ⅓ 来评估训练的模型。此外,对于每种拆分,目标特征已与其他特征分开,从而在下表中列出了四个文件名。
# 表 2.2 Boston-housing 数据集按文件名和内容划分的文件名
| 特征 (12 个) | 目标变量 (1 个) | |
|---|---|---|
| 训练 | train-data.csv | train-target.csv |
| 测试 | test-data.csv | test-target.csv |
为了将它们引入我们的应用程序,我们需要能够下载此数据并将其转换为适当类型和形状的张量。为此,波士顿住房项目在 data.js 中定义了一个类 BostonHousingDataset 。该类抽象了数据集流操作,提供了一个 API 来检索原始数据作为数字矩阵。在内部,该类使用公共开源 papaparse [45]库流式传输和解析远程 CSV 文件。加载并解析文件后,该库将向我们返回一个数字数组。然后使用与第一个示例相同的 API 将其转换为张量,如下面的清单 2.7 所示,这是 index.js 中经过精简的示例,以关注相关位。
# 清单 2.7 将 Boston-housing 数据转换为 index.js 中的张量
// Initialize a BostonHousingDataset object defined in data.js.
const bostonData = new BostonHousingDataset();
const tensors = {};
// Convert the loaded csv data, of type number[][] into 2d tensors.
export const arraysToTensors = () => {
tensors.rawTrainFeatures = tf.tensor2d(bostonData.trainFeatures);
tensors.trainTarget = tf.tensor2d(bostonData.trainTarget);
tensors.rawTestFeatures = tf.tensor2d(bostonData.testFeatures);
tensors.testTarget = tf.tensor2d(bostonData.testTarget);
};
// Trigger the data to load asynchronously once the page has loaded.
let tensors;
document.addEventListener(
'DOMContentLoaded',
async () => {
await bostonData.loadData();
arraysToTensors();
},
false
);
# 2.3.4 精确定义波士顿住房问题
现在,我们已经可以以所需的形式访问我们的数据了,现在是时候更精确地阐明我们的任务了。我们说过,我们想从其他领域预测房地产中位数(MEDV ),但我们将如何确定自己做得如何?我们如何才能将好的模型与更好的模型区分开?
我们在第一个示例中使用的指标 meanAbsoluteError 均等地计算所有错误。如果只有 10 个样本,并且我们对所有 10 个样本都做出了预测,那么我们对其中 9 个样本的预测是正确的,但是在第 10 个样本上有 30 个预测,则 meanAbsoluteError 将为 3(因为 30/10 为 3)。相反,如果我们对每个样本的预测都偏离 3,那么 meanAbsoluteError 仍将为 3。这种均等错误原则似乎是唯一显然正确的选择,但是除了 meanAbsoluteError 之外,还有其他选择损失指标的方式。
另一种选择是权衡大错误而不是小错误。我们可以取误差的平方而不是取绝对误差的平均值。
继续上面的案例研究和十个样本,这种均方误差(MSE)方法发现,每个示例(10 x 3² = 90)减少 3 的损失比仅一个示例(1 x 30² = 900)减少 30 的损失要低。由于对大错误的敏感性,平方误差比绝对误差对样本离群值的敏感性更高。使 MSE 最小化的优化器拟合模型将优先选择犯一些小错误的模型,而不是偶尔给出非常差的估计的模型。显然,两种误差测量都希望使用完全没有误差的模型!但是,如果您的应用程序可能对错误的异常值非常敏感,则 MSE 可能是比 MAE 更好的选择。还有其他一些技术原因可以选择 MSE 或 MAE,但目前它们并不重要。在此示例中,我们将使用 MSE。
在继续之前,我们应该找到损失的基线估计。如果我们从非常简单的估计中不知道错误,那么我们就没有能力从更复杂的模型中评估错误。我们将使用平均房地产价格作为“最佳猜测”的代表,并通过始终猜测该值来计算误差。
# 清单 2.8 计算猜测均价的基线损失(meanSquaredError)
export const computeBaseline = () => {
const avgPrice = tf.mean(tensors.trainTarget);
console.log(`Average price: ${avgPrice.dataSync()[0]}`);
const baseline = tf.mean(tf.pow(tf.sub(tensors.testTarget, avgPrice), 2));
console.log(`Baseline loss: ${baseline.dataSync()[0]}`);
};
TensorFlow.js 通过在 GPU 上进行调度来优化其计算,张量可能并不总是可由 CPU 访问。清单 2.8 中对 dataSync 的调用告诉 TFJS 完成张量的计算并将该值从 GPU 提取到 CPU 中,以便可以将其打印出来或与非张量流操作共享。
执行后,以上代码在控制台上产生以下内容:
Average price: 22.768770217895508
Baseline loss: 85.58282470703125
这告诉我们,错误率约为 85.58。如果我们要构建一个始终输出 22.77 的模型,则该模型将在测试数据上达到 85.58 的 MSE。同样,请注意,我们根据训练数据计算了指标,并根据测试数据进行了评估,以避免产生误差。
85.58 是平均平方误差,因此我们应该取平方根以获得平均误差。85.58 的平方根约为 9.25。因此,可以说我们期望我们的(常数)估计值平均偏离(高于或低于)大约 9.25。由于根据表 2.1 的价值以千美元为单位,因此这个估计常数意味着上下浮动约 9,250 美元。如果这对于我们的应用程序足够好,我们可以在这里停止!明智的机器学习从业者知道什么时候可以避免不必要的复杂性。假设我们的价格估算器应用程序需要比这更接近。我们将通过对数据拟合线性模型来看看是否可以实现比 85.58 更好的 MSE。
# 2.3.5 数据标准化
通过查看波士顿的住房功能,我们可以看到广泛的价值。NOX 介于 0.4 到 0.9 之间,而 TAX 则介于 180 到 711 之间。为适应线性回归,优化器将尝试查找每个特征的系数,以使这些特征的总和乘以系数将近似等于房屋价格。回想一下,要找到这些系数,优化器会在某空间梯度附近徘徊。如果某些特征系数比例比其他特征大一些,则这些特征将比其他特征敏感得多。一个方向很小的移动会比另一个方向的很大移动对输出影响更大。这可能会导致不稳定并使其难以拟合模型。
为了解决这个问题,我们首先将数据标准化。这意味着我们将对特征进行缩放,以使它们具有零均值和单位标准偏差。这种类型的归一化非常普遍,也可以称为标准转换或“ z 分数归一化”。这样做的算法很简单,我们首先计算每个特征的均值,然后从原始值中减去它,以便该特征的平均值为零。然后,我们用减去的平均值计算特征的标准偏差,然后除以该平均值。用伪代码:
normalizedFeature = (feature - mean(feature)) / std(feature)
例如,当 feature 为[10,20,30,40]时,规范化的版本将约为[-1.3,-0.4,0.4,1.3] ,其平均值显然为零,并且通过肉眼标准偏差约为 1 。在 Boston-housing 的示例中,将规范化代码分解到一个单独的文件 normalization.js 中,该文件的内容在 2.9 中列出。在这里,我们看到两个函数,一个函数从提供的 rank-2 张量计算平均值和标准差,另一个函数在给定提供的预先计算的均值和 std 的情况下标准化张量。
# 清单 2.9 数据归一化
/**
* Calculates the mean and standard deviation of each column of a data array.
*
* @param {Tensor2d} data Dataset from which to calculate the mean and
* std of each column independently.
*
* @returns {Object} Contains the mean and standard deviation of each vector
* column as 1d tensors.
*/
export function determineMeanAndStddev(data) {
const dataMean = data.mean(0);
const diffFromMean = data.sub(dataMean);
const squaredDiffFromMean = diffFromMean.square();
const variance = squaredDiffFromMean.mean(0);
const std = variance.sqrt();
return { mean, std };
}
/**
* Given expected mean and standard deviation, normalizes a dataset by
* subtracting the mean and dividing by the standard deviation.
*
* @param {Tensor2d} data: Data to normalize. Shape: [numSamples, numFeatures].
* @param {Tensor1d} mean: Expected mean of the data. Shape [numFeatures].
* @param {Tensor1d} std: Expected std of the data. Shape [numFeatures]
*
* @returns {Tensor2d}: Tensor the same shape as data, but each column
* normalized to have zero mean and unit standard deviation.
*/
export function normalizeTensor(data, dataMean, dataStd) {
return data.sub(dataMean).div(dataStd);
}
让我们深入研究这些功能。函数 determineMeanAndStddev 将张量用作输入数据。按照惯例,第一维是样本维度,每个索引对应一个独立的唯一样本。第二个维度是特征维度,因此 12 个元素对应于 12 个输入特征(例如 CRIM ,ZN ,INDUS 等)。由于我们要独立计算每个特征的均值,因此我们将 使用const dataMean = data.mean(0);
在此调用中,“ 0 ”表示均值应在第 0 个索引(即第一)维上进行。回想一下,数据是 2 级张量,因此具有二维(又称轴)。第一个轴是样品维度。当我们沿着此轴从第一个元素移动到第二个元素到第三个元素时,我们指的是不同的样本,或者在这个清净下,指的是不同的房地产。第二维是特征维。当我们从该维度的第一个元素移到第二个元素时,我们所指的是不同的功能,例如表 2.1 中的 CRIM ,ZN 和 INDUS 。当我们沿轴 0 取平均值时,我们就是在采样方向上取平均值。结果是仅保留特征轴的 1 级张量。我们掌握了每个特征的平均值。取而代之的是,如果取轴 1 的均值,则仍将获得 1 级张量,但其余轴将为样本维度。这些值将对应于每个房地产的平均值。使用轴时,请注意要朝正确的方向进行计算,这经常产生错误。
当然,如果我们在此处设置一个断点[46],则可以使用 JS 控制台探索计算出平均值,并且我们看到平均值非常接近于我们为整个数据集计算出的平均值。这意味着我们的训练样本具有代表性。
> dataMean.shape
[12]
> dataMean.print();
[3.3603415, 10.6891899, 11.2934837, 0.0600601, 0.5571442, 6.2656188, 68.2264328, 3.7099338, 9.6336336, 409.2792969, 18.4480476, 12.5154343]
在下一行中,我们从数据中减去(使用 tf.sub )平均值。
const diffFromMean = data.sub(dataMean);
如果您没有全力以赴,那么这条线可能隐藏了一段令人愉悦的小魔术。您会看到,data 是形状为[ 333,12 ] 的 2 级张量,而 dataMean 是形状[12] 的 1 级张量。通常,不可能减去两个具有不同形状的张量。但是,在这种情况下,TensorFlow 使用广播来扩展第二张量的形状,实际上是将其重复 333 次,从而完全按照用户的意图进行操作而无需将其拼写出来。获取可用性很方便,但有时形状兼容广播的规则可能会有些混乱。如果您对广播的详细信息感兴趣,请直接跳到下面的信息框 2.5。
determineMeanAndStddev 函数的接下来的几行没有新的惊喜。tf.square()是每个元素的平方,而 tf.sqrt()取每个元素的平方根。TensorFlow.js API 参考https://js.tensorflow.org/api/latest/中记录了每种方法的详细API 。文档页面还具有实时可编辑的小部件,使您可以探索函数如何使用自己的参数值,如图 2.12 所示。
在这个例子中, determineMeanAndStddev 方法可以更简洁地表示为:const std = data.sub(data.mean(0)).square().mean().sqrt();
您应该能够看到 TensorFlow 允许我们在无需太多代码的情况下表达很多计算。
# 图 2.12 js.tensorflow.org 上的 TensorFlow.js API 文档可让您直接在文档内浏览 TensorFlow API 并与之交互。这使得了解功能用途和棘手的边缘情况变得简单而快捷。
专栏 1.1 广播
考虑张量运算,例如 C = tf.someOperation(A,B),其中 A 和 B 是张量。如果可能,并且没有歧义,将广播较小的张量匹配较大张量的形状。广播包括两个步骤:
将轴(称为广播轴)添加到较小的张量以匹配较大张量的等级。
在这些新轴旁边会重复出现较小的张量,以匹配较大张量的完整形状。
在实现方面,实际上不会创建新的张量,因为这将非常低效。重复操作完全是虚拟的,它发生在算法级别而不是内存级别。但是,考虑到沿着新轴重复的较小张量是一个有用的思维模型。
在广播中,如果一个张量的形状为(a,b,…,n,n + 1,…m),而另一个张量的形状为(n,n + 1,…,m),则通常可以应用两张量元素运算。 )。然后,广播将自动从轴 a 到 n-1 发生。例如,以下示例通过广播将元素级最大运算应用于不同形状的两个随机张量。
x = tf.randomUniform([64,3,11,9]); #A
y = tf.randomUniform([11,9]); #B
z = tf.maximum(x,y); #C
#A x 是形状为[64、3、11、9]的随机张量。
#B y 是形状为[11,9]的随机张量。
#C 输出 z 具有 x 的形状[64,3,11,9].
# 2.3.6 波士顿住房数据的线性回归
我们的数据已标准化,我们已经完成了数据处理工作,以计算出合理的基线-下一步是建立并拟合模型,以查看我们是否能跑赢基线。在下面的清单 2.10 中,我们定义了线性回归模型,就像在 2.1 节中所做的那样。代码非常相似;我们从下载时间预测模型中看到的唯一区别是在 inputShape 配置中,该配置现在接受长度为 12 的向量,而不是 1。单个密集层仍具有单位:1 ,指示输出一个数字。
# 清单 2.10 为波士顿住房定义线性回归模型(来自 index.js)
export const linearRegressionModel = () => {
const model = tf.sequential();
model.add(tf.layers.dense({ inputShape: [bostonData.numFeatures], units: 1 }));
return model;
};
回想一下,在定义了模型后,开始训练之前,我们必须通过调用 model.compile 来指定损失和优化器。在清单 2.11 中,我们看到指定了“ meanSquaredError” 损失,并且优化器正在使用自定义的学习率。在我们之前的示例中,optimizer 参数设置为字符串'sgd' ,但是现在它是 tf.train.sgd(学习率)。此函数将返回一个对象,该对象表示 SGD 优化算法,使用我们的自定义学习率进行了参数设置。这是 TensorFlow.js 中的一种常见模式,是从 Keras 借来的,您将看到它被许多可配置选项采用。对于标准的众所周知的默认参数,字符串哨兵值可以替代所需的对象类型,而 TensorFlow.js 将使用默认参数替代所需对象的字符串。在这种情况下,“ sgd” 将替换为 tf.train.sgd(0.01)。如果需要其他自定义,则用户可以通过工厂模式构建对象,并提供所需的自定义值。这使代码在大多数情况下都简洁明了,但允许高级用户在需要时覆盖默认行为。
# 清单 2.11 用于波士顿住房的模型编译(来自 index.js)
const LEARNING_RATE = 0.01;
model.compile({ optimizer: tf.train.sgd(LEARNING_RATE), loss: 'meanSquaredError' });
现在我们可以使用训练数据集训练模型。在清单 2.12 到 2.14 中,我们将使用 model.fit()调用的一些附加功能,但实际上它的作用与图 2.6 相同。在每个步骤中,它从特征(tensors.trainFeatures )和目标(tensors.trainTarget )中选择许多新样本,计算损失,然后更新内部系数以减少损失。该过程将重复 NUM_EPOCHS 次训练数据,并在每个步骤中选择 BATCH_SIZE 个样本。
# 清单 2.12 在波士顿住房数据上训练模型
await model.fit(tensors.trainFeatures, tensors.trainTarget, {
batchSize: BATCH_SIZE
epochs: NUM_EPOCHS,
});
在波士顿住房应用中,我们演示了模型训练时训练损失的图表。这需要使用 model.fit()的回调功能来更新 UI。所述 model.fit()回调 API 允许用户提供回调函数,这将在特定事件被执行。从 0.12.0 版本开始,回调触发器的完整列表是 onTrainBegin ,onTrainEnd ,onEpochBegin ,onEpochEnd ,onBatchBegin 和 onBatchEnd 。
# 清单 2.13 model.fit 中的回调
let trainLoss;
await model.fit(tensors.trainFeatures, tensors.trainTarget, {
batchSize: BATCH_SIZE,
epochs: NUM_EPOCHS,
callbacks: {
onEpochEnd: async (epoch, logs) => {
await ui.updateStatus(`Epoch ${epoch + 1} of ${NUM_EPOCHS} completed.`);
trainLoss = logs.loss;
await ui.plotData(epoch, trainLoss);
}
}
});
验证是机器学习的一个概念。在上面的下载时间示例中,我们希望将训练数据与测试数据分开,因为我们希望对模型在新的看不见的数据上的表现进行无偏估计。但是,经常发生的是还有另一个拆分称为验证数据。验证数据与训练数据和测试数据分开。验证数据做什么用?ML 工程师将在验证数据上看到结果,并使用该结果来更改模型的某些配置[47],以提高验证数据的准确性。这一切都很好。但是,如果此循环完成了足够的次数,那么我们实际上是在验证数据上进行调整。如果我们使用相同的验证数据来评估模型的最终准确性,则最终评估的结果将不再可以推广,因为模型已经看到了数据并且不能保证评估的结果能够反映模型处理将来那些看不见的数据。这是将验证与测试数据分开的目的。我们的想法是使我们的模型适合训练数据,并基于对验证数据的评估来调整模型的超参数。当我们全部完成并对该过程感到满意时,我们只需对测试数据进行一次模型评估即可获得最终的,可概括的性能评估。下面我们总结训练集,验证集和测试集,以及如何在 TensorFlow.js 中使用它们。
并非所有项目都将使用所有三种类型的数据。通常,快速勘探或研究项目将仅使用训练和验证数据,而不会为测试保留一组“纯”数据。虽然不太严格,但这有时是有限资源的最佳使用。
- 训练数据:使用梯度下降拟合模型系数。
- 在 TensorFlow.js 中的用法:通常,训练数据使用主要参数(x 和 y )来调用 Model.fit(x,y,config)。
- 验证数据:用于选择模型结构和超参数。
- TensorFlow.js 中的用法:Model.fit()有两种指定验证数据的方式,它们都是 config 参数。如果您(用户)具有用于验证的显式数据,则可以将其指定为 config.validationData 。相反,如果您希望框架拆分一些训练数据并将其用作验证数据,请在 config.validationSplit 中指定要使用的分数。该框架将注意不要使用验证数据来训练模型,因此不会有重叠。
- 测试数据:对模型性能的最终无偏估计。
- TensorFlow.js 中的用法:通过将评估数据作为 x 和 y 参数传递给 Model.evaluate(x,y,config)来向系统公开评估数据。
在清单 2.14 中,验证损失与训练损失一起计算。所述 validationSplit:0.2 字段表示选择训练数据的最后 20%作为验证数据来使用。此数据将不会用于训练(它不会影响梯度下降)。
# 清单 2.14 包括验证数据的 model.fit
let trainLoss;
let valLoss;
await model.fit(tensors.trainFeatures, tensors.trainTarget, {
batchSize: BATCH_SIZE,
epochs: NUM_EPOCHS,
validationSplit: 0.2,
callbacks: {
onEpochEnd: async (epoch, logs) => {
await ui.updateStatus(`Epoch ${epoch + 1} of ${NUM_EPOCHS} completed.`);
trainLoss = logs.loss;
valLoss = logs.val_loss;
await ui.plotData(epoch, trainLoss, valLoss);
}
}
});
在浏览器中,将此模型训练到 200 个循环大约需要 11 秒钟。现在,我们可以在测试集中评估模型,以查看它是否比基线更好。清单 2.15 显示了如何使用model.evaluate()来收集我们保留的测试数据上的模型性能,然后调用我们的自定义 UI 例程来更新视图。
# 清单 2.15 在测试数据上评估我们的模型并更新 UI(来自 index.js)
await ui.updateStatus('Running on test data...');
const result = model.evaluate(tensors.testFeatures, tensors.testTarget, { batchSize: BATCH_SIZE });
const testLoss = result.dataSync()[0];
await ui.updateStatus(
`Final train-set loss: ${trainLoss.toFixed(4)}\n` +
`Final validation-set loss: ${valLoss.toFixed(4)}\n` +
`Test-set loss: ${testLoss.toFixed(4)}`
);
在这里,model.evaluate()返回一个标量,其中包含在测试集上计算的损失。
由于梯度下降的随机性,您可能会得到不同的结果,但是以下结果是典型的:
- 最终训练集损失:21.9864
- 最终验证集损失:31.1396
- 测试集损失:25.3206
- 基准损失: 85.58
由此可见,我们对损失的最终无偏估计约为 25.3,这比我们的 85.6 基准要好得多。回想一下,我们的损失是使用 meanSquaredError 计算的。取平方根,我们看到基线估计值通常偏离 9.2 以上,而线性模型仅偏离约 5.0。很大的进步!如果我们是世界上唯一可以访问此信息的人,那么我们可以成为 1978 年波士顿最好的房地产投资者!除非使用其他更有效的方式,否则没人能够建立更准确的估算…
如果您满怀好奇心,单击“训练神经网络回归器”,便知道”可能”更好的估计。在下一章中,我们将介绍非线性深度模型,以说明如何实现这种壮举。
